42 Mallas para cálculos numéricos con NumPy

¡Bienvenide al mundo de la visualización de datos con meshgrid en Python! Esta es tu entrada a una herramienta que te permitirá crear mallas de coordenadas para visualizar datos en dos y tres dimensiones de manera efectiva. A través de meshgrid, aprenderás a transformar vectores unidimensionales en matrices de coordenadas, brindándote la capacidad de diseñar gráficos a medida y analizar conjuntos de datos complejos.

Usarás meshgrid para construir mallas, así como para evaluar funciones sobre diversos rangos de valores. Esto te facilitará la generación de representaciones gráficas que muestren tus datos con precisión y claridad. Al concluir, tendrás una visión clara de cómo meshgrid puede ser usado en tu análisis de datos.

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# Creando dos rangos de valores
x = np.linspace(-5, 0, 10)
y = np.linspace(-5, 5, 10)
X, Y = np.meshgrid(x, y)

array([-5.        , -4.44444444, -3.88888889, -3.33333333, -2.77777778,
       -2.22222222, -1.66666667, -1.11111111, -0.55555556,  0.        ])

array([[-5.        , -4.44444444, -3.88888889, -3.33333333, -2.77777778,
        -2.22222222, -1.66666667, -1.11111111, -0.55555556,  0.        ],
       [-5.        , -4.44444444, -3.88888889, -3.33333333, -2.77777778,
        -2.22222222, -1.66666667, -1.11111111, -0.55555556,  0.        ],
       [-5.        , -4.44444444, -3.88888889, -3.33333333, -2.77777778,
        -2.22222222, -1.66666667, -1.11111111, -0.55555556,  0.        ],
       [-5.        , -4.44444444, -3.88888889, -3.33333333, -2.77777778,
        -2.22222222, -1.66666667, -1.11111111, -0.55555556,  0.        ],
       [-5.        , -4.44444444, -3.88888889, -3.33333333, -2.77777778,
        -2.22222222, -1.66666667, -1.11111111, -0.55555556,  0.        ],
       [-5.        , -4.44444444, -3.88888889, -3.33333333, -2.77777778,
        -2.22222222, -1.66666667, -1.11111111, -0.55555556,  0.        ],
       [-5.        , -4.44444444, -3.88888889, -3.33333333, -2.77777778,
        -2.22222222, -1.66666667, -1.11111111, -0.55555556,  0.        ],
       [-5.        , -4.44444444, -3.88888889, -3.33333333, -2.77777778,
        -2.22222222, -1.66666667, -1.11111111, -0.55555556,  0.        ],
       [-5.        , -4.44444444, -3.88888889, -3.33333333, -2.77777778,
        -2.22222222, -1.66666667, -1.11111111, -0.55555556,  0.        ],
       [-5.        , -4.44444444, -3.88888889, -3.33333333, -2.77777778,
        -2.22222222, -1.66666667, -1.11111111, -0.55555556,  0.        ]])

array([[-5.        , -5.        , -5.        , -5.        , -5.        ,
        -5.        , -5.        , -5.        , -5.        , -5.        ],
       [-3.88888889, -3.88888889, -3.88888889, -3.88888889, -3.88888889,
        -3.88888889, -3.88888889, -3.88888889, -3.88888889, -3.88888889],
       [-2.77777778, -2.77777778, -2.77777778, -2.77777778, -2.77777778,
        -2.77777778, -2.77777778, -2.77777778, -2.77777778, -2.77777778],
       [-1.66666667, -1.66666667, -1.66666667, -1.66666667, -1.66666667,
        -1.66666667, -1.66666667, -1.66666667, -1.66666667, -1.66666667],
       [-0.55555556, -0.55555556, -0.55555556, -0.55555556, -0.55555556,
        -0.55555556, -0.55555556, -0.55555556, -0.55555556, -0.55555556],
       [ 0.55555556,  0.55555556,  0.55555556,  0.55555556,  0.55555556,
         0.55555556,  0.55555556,  0.55555556,  0.55555556,  0.55555556],
       [ 1.66666667,  1.66666667,  1.66666667,  1.66666667,  1.66666667,
         1.66666667,  1.66666667,  1.66666667,  1.66666667,  1.66666667],
       [ 2.77777778,  2.77777778,  2.77777778,  2.77777778,  2.77777778,
         2.77777778,  2.77777778,  2.77777778,  2.77777778,  2.77777778],
       [ 3.88888889,  3.88888889,  3.88888889,  3.88888889,  3.88888889,
         3.88888889,  3.88888889,  3.88888889,  3.88888889,  3.88888889],
       [ 5.        ,  5.        ,  5.        ,  5.        ,  5.        ,
         5.        ,  5.        ,  5.        ,  5.        ,  5.        ]])

# Visualizando la malla con un gráfico de dispersión
fig, ax = plt.subplots()
ax.scatter(X, Y)

Z = X**2 + Y**2
Z

array([[50.        , 44.75308642, 40.12345679, 36.11111111, 32.71604938,
        29.9382716 , 27.77777778, 26.2345679 , 25.30864198, 25.        ],
       [40.12345679, 34.87654321, 30.24691358, 26.2345679 , 22.83950617,
        20.0617284 , 17.90123457, 16.35802469, 15.43209877, 15.12345679],
       [32.71604938, 27.4691358 , 22.83950617, 18.82716049, 15.43209877,
        12.65432099, 10.49382716,  8.95061728,  8.02469136,  7.71604938],
       [27.77777778, 22.5308642 , 17.90123457, 13.88888889, 10.49382716,
         7.71604938,  5.55555556,  4.01234568,  3.08641975,  2.77777778],
       [25.30864198, 20.0617284 , 15.43209877, 11.41975309,  8.02469136,
         5.24691358,  3.08641975,  1.54320988,  0.61728395,  0.30864198],
       [25.30864198, 20.0617284 , 15.43209877, 11.41975309,  8.02469136,
         5.24691358,  3.08641975,  1.54320988,  0.61728395,  0.30864198],
       [27.77777778, 22.5308642 , 17.90123457, 13.88888889, 10.49382716,
         7.71604938,  5.55555556,  4.01234568,  3.08641975,  2.77777778],
       [32.71604938, 27.4691358 , 22.83950617, 18.82716049, 15.43209877,
        12.65432099, 10.49382716,  8.95061728,  8.02469136,  7.71604938],
       [40.12345679, 34.87654321, 30.24691358, 26.2345679 , 22.83950617,
        20.0617284 , 17.90123457, 16.35802469, 15.43209877, 15.12345679],
       [50.        , 44.75308642, 40.12345679, 36.11111111, 32.71604938,
        29.9382716 , 27.77777778, 26.2345679 , 25.30864198, 25.        ]])

Z.shape

(10, 10)

# Creando la figura y el eje para el gráfico 3D usando subplots
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})

# Dibujando la superficie
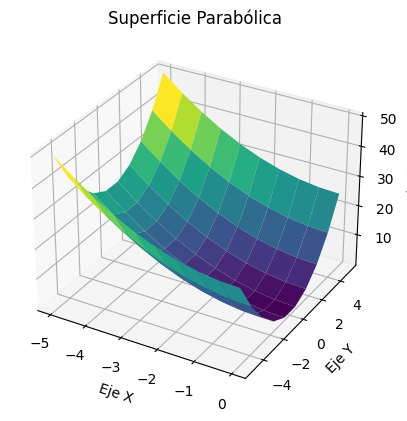
surf = ax.plot_surface(X, Y, Z, cmap='viridis')

# Etiquetas y título
ax.set_xlabel('Eje X')
ax.set_ylabel('Eje Y')
ax.set_zlabel('Eje Z')
ax.set_title('Superficie Parabólica')

Text(0.5, 0.92, 'Superficie Parabólica')